This gallery contains 5 photos.
I took a trip home in September to visit family in Connecticut. Here’s a few pictures from Ender’s State Forest.
This gallery contains 5 photos.
I took a trip home in September to visit family in Connecticut. Here’s a few pictures from Ender’s State Forest.
Those of you who know me in real life know that I am a gamer. I’ve been playing board games of various sorts since I was a kid; Dungeons & Dragons and its ilk since high school; and LARPing (boffer and not) since college. Yes, I’ve somehow become even MORE nerdy as I’ve aged. Chalk it up to the friends I’ve made through gaming. Gamers, as we know, tend to attract more gamers. We flock together, able to talk to each other about our shared passion. And through that conversation, we discover new games and new ways to connect with our fellows. One of the side effects of this is a near-continuous (at least for me) hemorrhaging of money into the hobby as we discover new things. Over the years I’ve backed more than my fair share of Kickstarter campaigns for new games from various designers and companies, ranging from massive new RPG products like Numenera and Shadows of Esteren to simple things like Pairs. So, of course, when I found out about Cheapass Games‘ Kickstarter for Tak, based on the books of Patrick Rothfuss’s Kingkiller Chronicle, I had to go take a look.

Gaming is why I don’t have any money.
Holy crap, this game is beautiful. The core idea is incredibly simple: You’re trying to make a path from one side of the board to the other by placing pieces of your color, while trying to prevent your opponent from doing the same. To do this, you can either place a piece or move one of your pieces (or stacks of pieces). That’s it. This video shows you the rest of the rules. It’s simple, elegant, and easy to learn. Then you start to play it, and you realize just how complex it can become, and how quickly things can turn around in the game. You can play it on any size board, from 3×3 on up. The beta rules provided as part of the Kickstarter go up to an 8×8, with some uncertainty as to the piece counts for a 7×7 board (saying that it’s an uncommon size).

WHAT DO YOU MEAN, “IT ONLY GOES TO 8?!?!?!”
Being that I’m an engineer, and that I get paid to do math, I figured I’d do a little math to see what I could figure out about Tak. Because yes, I do math at things for fun sometimes.
Let’s start with the basics. I put together a table of data based on the beta rules available on Cheapass Games’ website:
| Side Length | Spaces | Pieces per Player | Capstones per Player | Total Pieces | Total Capstones |
| 3 | 9 | 10 | 0 | 20 | 0 |
| 4 | 16 | 15 | 0 | 30 | 0 |
| 5 | 25 | 21 | 1 | 42 | 2 |
| 6 | 36 | 30 | 1 | 60 | 2 |
| 7 | 49 | 40 | 2* | 80 | 4* |
| 8 | 64 | 50 | 2 | 100 | 4 |
*Note that I’m going to just assume for ease of calculations that when you’re playing on a 7×7 board you get 2 capstones. It just makes sense to me with the pattern of the previous sizes: Every 2 extra spaces on a side gets an additional capstone. 3-4 gets zero, 5-6 gets one, 7-8 gets two, etc. Plus, as you’ll see soon, the math works out so beautifully.
From that table of basic information, I pulled out a few pieces of derived data to further expand what I could work with mathematically:
| Side Length | Total Pieces – Spaces | Total Pieces/Spaces | Spaces/Capstone |
| 3 | 11 | 2.22 | – |
| 4 | 14 | 1.88 | – |
| 5 | 17 | 1.68 | 25 |
| 6 | 24 | 1.67 | 36 |
| 7 | 31 | 1.63 | 24.5 |
| 8 | 36 | 1.56 | 32 |
“Okay, Josh,” you say, “that’s neat and all, but what does it mean?” It means, dear reader, that we can figure out how to play on any size board we want. First, let’s take an actual look at these data. They make much more sense in graphical form:
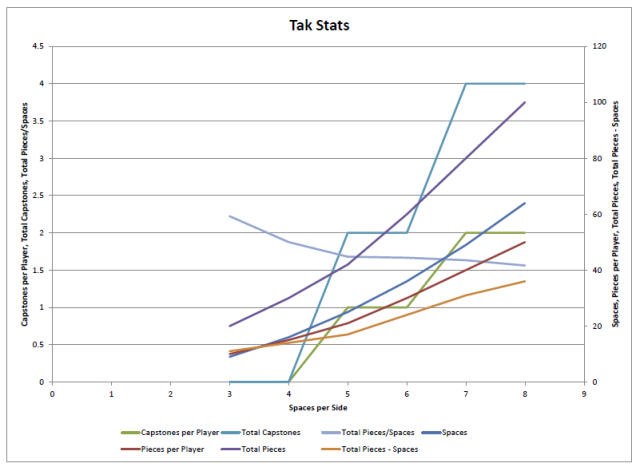
Okay, maybe they don’t…
So, what exactly are we looking at? The short answer is that it’s a mix of useful and superfluous information that, when examined under-*ducks thrown vegetables* All right, all right! We can use numerical analyses to figure out the slopes of the lines representing Pieces Per Player, Total Pieces, Total Pieces/Spaces, and Total Pieces – Spaces. By doing this, and then projecting the curves out to higher numbers of spaces per side, we can get a good idea of how many pieces would be needed to play games on those size boards. I say “a good idea” because, well, this is what the projections look like:
| Side Length | Spaces | Pieces per Player |
| 9 | 81 | 59 |
| 10 | 100 | 71 |
| 11 | 121 | 83 |
| 12 | 144 | 96 |
| 13 | 169 | 109 |
| 14 | 196 | 124 |
| 15 | 225 | 139 |
| 16 | 256 | 154 |
| 17 | 289 | 171 |
| 18 | 324 | 188 |
| 19 | 361 | 205 |
| 20 | 400 | 224 |
| 21 | 441 | 243 |
| 22 | 484 | 262 |
| 23 | 529 | 282 |
| 24 | 576 | 303 |
Kind of ugly numbers for the piece counts, right? The space counts are what they are, but we can round the piece counts to look a little bit nicer. We can also project out the number of capstones, using the formula I described earlier (+1 capstone for every 2 added spaces on a side). This gives the following table:
Side Length |
Rounded Pieces per Player |
Capstones per Player |
Total Pieces |
Total Capstones |
Total Pieces/ Spaces |
Spaces/ Capstone |
| 3 | 10 | 0 | 20 | 0 | 2.22 | – |
| 4 | 15 | 0 | 30 | 0 | 1.88 | – |
| 5 | 21 | 1 | 42 | 2 | 1.68 | 25 |
| 6 | 30 | 1 | 60 | 2 | 1.67 | 36 |
| 7 | 40 | 2 | 80 | 4 | 1.63 | 24.5 |
| 8 | 50 | 2 | 100 | 4 | 1.56 | 32 |
| 9 | 60 | 3 | 120 | 6 | 1.481 | 27 |
| 10 | 70 | 3 | 140 | 6 | 1.4 | 33.33 |
| 11 | 85 | 4 | 170 | 8 | 1.41 | 30.25 |
| 12 | 95 | 4 | 190 | 8 | 1.32 | 36 |
| 13 | 110 | 5 | 220 | 10 | 1.302 | 33.8 |
| 14 | 125 | 5 | 250 | 10 | 1.28 | 39.2 |
| 15 | 140 | 6 | 280 | 12 | 1.24 | 37.5 |
| 16 | 155 | 6 | 310 | 12 | 1.21 | 42.67 |
| 17 | 170 | 7 | 340 | 14 | 1.176 | 41.29 |
| 18 | 190 | 7 | 380 | 14 | 1.173 | 46.29 |
| 19 | 205 | 8 | 410 | 16 | 1.136 | 45.125 |
| 20 | 225 | 8 | 450 | 16 | 1.125 | 50 |
| 21 | 245 | 9 | 490 | 18 | 1.11 | 49 |
| 22 | 260 | 9 | 520 | 18 | 1.074 | 53.78 |
| 23 | 280 | 10 | 560 | 20 | 1.059 | 52.9 |
| 24 | 300 | 10 | 600 | 20 | 1.042 | 57.6 |
What a god-awful mess! Visually, it absolutely is (I’m an engineer, not a graphic designer!). Mathematically, it’s quite beautiful. All of these things are described by simple, well-fitted formulas that can be easily projected out for any size of Tak board, pretty much indefinitely:
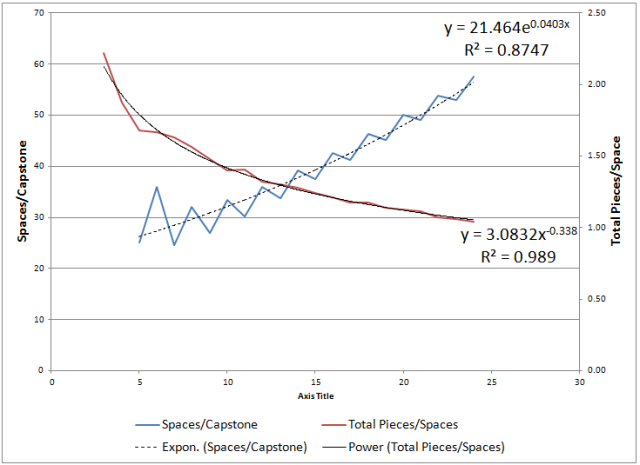
I told you the math was pretty! A power curve and an exponential curve tell you how many pieces you have to split between the players and the number of capstones each player gets. If you use my numbers from the first projection chart (the one where I didn’t round the number of pieces) you can easily calculate the base formulas yourself using Excel, Google Sheets, or something similar. I’ll happily answer questions if you have them.
So there you have it! Now you can play Tak on any size board you could possibly want to! Of course, whether it’s a good idea to play a 20×20 game of Tak (or bigger!) is a completely different question. With 225 pieces and 8 capstones per player, that’s going to be one long game. That said, it’d definitely be an interesting one!
One last thing: While I’m sure most people will understand this implicitly, I’m going to state it for the record: Tak is owned by Cheapass Games. It was created by James Ernest and Patrick Rothfuss. I don’t have any rights to the game, nor am I claiming any rights to it. This post is entirely speculative and should not in any way, shape, or form be thought of as official Tak rules. This post is not endorsed or authorized by Cheapass Games in any way, and no offense is meant to them. I’m just a fan of their work who decided to go a little crazy. So there you go. Now go back the Tak Kickstarter! Play the game! Make your own set! Drink while playing the game! It makes it more fun! (Please drink responsibly. This means don’t try making a wooden set using power tools if inebriated, among other things. Don’t be an idiot, m’kay?)
Usually I like to talk about beer. Today I’m going to talk about something that is not beer. Today I’m going to talk about something that made me, as an engineer and rational adult, incredibly angry.
There is a town in Texas called Irving. There is a small boy who lives there. He seems like a neat kid, from what I’ve read about him. He’s smart. He like to play with robots. He likes to build electronic stuff to see what he can make. He made a clock at home with a circuit board. It had a digital clock display, and a digital battery display. He took it to school to show his teachers, because he was proud of his accomplishment.
When his English teacher saw it, they had him arrested, because they thought it might have been a bomb. Even though he told them it was a clock. He told everyone who saw it that it was a clock. Everyone who looked at it agreed it was a clock. But he was still arrested and suspended, because it looked like it could have been a bomb.
Did I mention that this kid’s name is Ahmed Mohamed?
Excuse me while I rage for a few minutes. While I do that, you should read what Ken White at Popehat wrote about this. He’s more articulate than I’m about to be.
Okay, you read it? Great. Now, will the Irving, TX police department and school administration please…
What the actual fuck is wrong with these police and administrators? Can they not hear themselves talk? Did their parents beat any and all common sense out of them when they were children? Did all of them fail shop class? And don’t give me any bullshit about how they didn’t have the chance to take shop, I’m pretty sure everyone involved in this situation is old enough that shop class was still offered, if it was offered in my podunk hometown.
The school system, the prosecutor’s office, the town, and the police department have likely all opened themselves up to lawsuits, and quite frankly I hope they get taken to the cleaners. Everyone involved with this horrible chain of decisions deserves to be fired. None of them, to my mind, are qualified to serve as dogcatcher, let alone in positions of authority and responsibility such as these.
I am an engineer. I did shit like this all the time when I was a kid. No one ever freaked out about it, no one ever called the police about it. Of course, I also happen to be white, with about as white a name as you can get, and I grew up mostly before 9/11, so OF COURSE it wasn’t an issue. I would bet dollars to doughnuts that if it was a white kid named John Smith who brought his homemade electronic clock to school in Irving, TX, he would have gotten extra credit for it in his science class, not gotten arrested. But because this poor kid is named Ahmed Mohamed, he got the full paranoid racist treatment. Because why on earth would a Muslim kid build something electronic if it WASN’T a bomb, right?
For our less astute readers, namely the Irving, TX law enforcement community and school administration, that last sentence is sarcasm. At your expense. Because you’re all fucking morons.
Goddammit, Texas. Grow the fuck up and join the twenty-first goddamned century. The grownups are tired of your bullshit.
So. It’s, uh, been awhile. A year, in fact, since I wrote anything on here.
Yup. That’s awhile, for sure.
But I’m back now! And boy, do we have some catching up to do. There’s so much stuff I have to write about, so many things to comment on…
*scans several news articles about Trump, police shootings, corporate corruption, and the Greek financial crises*
Um. Wow. Okay, we’ll come back to all that. In the meantime, here’s a picture of my cats to tide you over:
I finished the blanket chest. After nearly a year, a few dozen hours of actual work, a ton of self-doubt and self-loathing, and plenty of trial and error, it is done.
Those of you who’ve followed this blog for a while know that I’m really, really, really bad at getting stuff done that I say I’m going to do. Like for serious, it’s terrible. I originally started this blanket chest last year to give as a wedding gift to friends of mine who were getting married last September. Needless to say, it didn’t get done in time, and continued to not get done because of a bunch of personal stuff that was only exacerbated by my failure to finish the chest. But I pulled myself out of that funk and got it done. And now, I’m going to share it with you, dear readers, in all its hand-made glory.
Doesn’t look like much from the outside, does it? It really isn’t anything that special. It’s made of 100% clear white pine (which costs a bundle; I’ll go with #2 next time and just get the least knotty stuff I can if I make one for myself), finished with boiled linseed oil and paste wax, and held together with nails. However, when you get into the details, it’s a bit more complex than it looks.
First, let’s look at how this thing is put together. This is the front of the chest. You can see if you look at the picture above that there is a glue joint in the front panel running from side to side about 4 inches from the top. There’s actually a glue joint in every panel used to make this chest. The pieces were glued up and then cut specifically so that the glue joints would be in places where maximum strength was assured. While the location of the glue joints for the front, bottom, and sides wasn’t that important, for the top and back it was. The panels are all about 16″ wide, made up of a 1×12 and 1×4 board glued together. The stress on the back and top when the top is lifted could theoretically cause the glue to eventually fail. Because of that, I placed the glue joint towards the front of the top and towards the bottom of the back. That way the joints would be as un-stressed as possible when the top is lifted. You can see the glue joint in the top panel the in the next picture:

3 of the key design elements of the chest: Cleats, nails, and rabbets. Boot jacks are just for show.
As the caption says, there are 3 other important design elements exhibited here: The cleats, the nails, and the panel rabbets. The cleats are the strips of wood nailed to the ends of the top panel. They serve a dual purpose: keeping the lid from warping and helping keep the lid from splitting apart. They’re not glued in place, however. They, like the carcase of the chest itself, are nailed. Specifically, with clinched nails. The nails are driven in place and then bent over to hook them into the top of the lid. This keeps them place even if the wood shrinks and dries over time. The lack of glue allows for the wood to move as the humidity changes, which is critical to keep the lid in one piece.
The rest of the carcase is the same way: It’s nailed together, with no glue except in the panels. As in the lid, the nails allow for the wood to move as it dries and the humidity changes over the course of years. Were the panels glued together, even with screws, there would be a high chance of the glue failing over the years, or of the panels cracking.
The last key element is the panel rabbets. The front and back, as you can see, are a bit thinner on the ends than the rest of the wood used in this project. That’s because there are rabbets cut on the ends and bottom of each panel to allow the case to more easily be fitted together prior to nailing. This makes the case easier to clamp up and makes the joints more rigid. What’s not visible is the dadoes that were cut along each end board for the bottom of the chest to fit in. In this way, the bottom is secured both with nails and with the dadoes. It’s quite sturdy, all in all.
So let’s get to the next important part: Hinges. I used a set of locking hinges from Lee Valley. I forget the exact part number. They’re nice and easy to install. No mortising required, just screw them in place and you’re good to go. I used 7/8″ No. 8 screws and didn’t drill pilot holes. Pine is soft enough that you really don’t need them. I did have to re-do one side, though, when my measurements didn’t quite match the shape of the board. Oops. But it worked!
You can also see that my rabbet cuts were…less than flush. I did every single cut by hand. Every. Single. One. Next time, I’m going to use my router (which I didn’t have when I did these panels). I wanted to do this one completely by hand if I could, though. I wanted to know that I had the skills if I ever ended up needing them.
This project was a wonderful learning experience for me. I built a beautiful piece of furniture for some dear friends that will hopefully last them for many, many years; I learned a ton of new hand tool skills; and I think most importantly I started the process of rebuilding my self-esteem that’s been dangerously low for most of my life. I think this last picture sums up my feelings upon completing this chest pretty well:
So until next time, keep on pluggin’ away. Happy brewing!
Skål!
I’ve started collaborating with a bunch of good friends on a new side project, Hot Glue and Hope. My first post there is up today. In it, I show you how to make a cheese board using only hand tools that you can give as a gift or keep for yourself. The best part is that you can do it in only a couple of hours. Go check it out!
Happy reading!
Skål!
As I mentioned last week, I am absolutely terrible at getting projects completed on schedule and on time. I inevitably wait until the last possible second to start something, and usually wind up with an inferior product because of it. Sometimes that’s not the case, but more often than not it is. My greatest offense in recent months has been a large blanket chest that I started last August as a gift for two friends of mine who were getting married…in September. That chest is still incomplete as of this writing. How did it come to this? How has it been nearly a year, and the damn thing still isn’t done? Quite simple: Side projects and procrastination.
Last year I was just getting started with my forays into woodworking. I had refurbished a few hand tools, learned to properly use a hand plane (or thought I had!), and was well on my way to acquiring all the tools I’d need to be able to make some amazing stuff. I felt good about life. Then I started looking for a house, where I could have all the space I’d ever need to make said amazing stuff. Great! Of course, the house hunt took time, and the work space I had in the house I was living in was shared space, so I didn’t always have use of it when I might want to. That’s part of living with other people, and it’s a normal part of life. I also had a lot of other things going on in my life. But that didn’t stop me.
When I found out that my buddy Chris was getting married, I decided that I wanted to make him a wedding gift that would be useful for many years. A blanket chest seemed an obvious choice. Sturdy, large, and practical, they also can look very nice when properly made. I found plans for one online that could be made (they said) entirely with hand tools. This was an important thing to me at the time, since I lacked any power tools that would be remotely useful in building something so large. (Not actually true, I own an electric drill, which could have been used, but I didn’t. More on that later.)
I read the plans, made my list of things to buy, and headed out to make the purchases.
I went out to my local home center and purchased several boards of clear 3/4″ thick white pine. Knowing what I now know about lumber, I probably could have gotten this for MUCH less money had I taken the time to just go to a local sawmill or lumberyard and bought it there. Sure, I’d have had more work to do in milling the boards down to size before I could use them, but I would have saved upwards of half the cost! I also ordered 2 different kinds of cut nails from Lee Valley, one in black oxide finish and bulky, for actually putting the chest together, and a pound of smaller, unfinished ones, to be used for attaching the battens and any molding that I would put on in the end (which didn’t happen, but we’ll get to that). I also ordered some hinges. The parts thus assembled, I got to work.
I took the boards I bought and glued them together along the edges to make larger panels that would form the sides, bottom, and top of the the chest. The ends were made from shorter lengths of the panels. Prior to gluing, I had to use my jointer plane on the edges of the boards to get them smoothed and straight for gluing. A couple of days and much Titebond III later, I had my panels.
The particular design I was making called for cutting rabbets on the ends and bottoms of both side panels to give the ends and bottom of the chest something to latch on to, helping with both stability after construction and increasing the ease of actually putting the chest together in the first place. To make them, I used a combination of a backsaw, chisels, a cheap shoulder plane, and a router plane for final clean up. Calling them “ugly” would be a massive understatement. They were awful. Rough, uneven, and out of square. But they were rabbets! I then used my backsaw, chisel, and router plane to cut the dadoes in the end panels. With all the joinery cuts completed, and still a month before the wedding, I figured I would have plenty of time to finish it. Boy, was I wrong.
Of course, me being me, lots of little stuff happened that prevented me from getting the chest done in time.
Okay, that’s a lie. I was lazy and didn’t work on it. The idea of putting such a huge piece together, all by myself, was intimidating. I’d never used cut nails before! What if I screwed up? I’d have to start over! What if I drilled wrong, what if I didn’t cut the molding right, what if, what if, what if?
I was paralyzed by that fear of failure. So much so, in fact, that I put the boards away in a stack and didn’t touch them again for almost 6 months. They stayed essentially put until spring. I kept giving Chris excuses, kept on apologizing. And Chris, being the awesome dude he is, just grinned and nodded. I’m pretty sure he figured he’d get the chest about the time he was getting ready to retire, and he was okay with that. He’s known me long enough to know how I operate, so I don’t think he was surprised when I didn’t have the chest done in time for his wedding. I know that I was disappointed in me, though.
So early this spring, when I was finally moving into the house I’d bought, I deliberately put the boards out in the basement where I would have no choice but to look at them. They would be a constant reminder that, “Hey, you’ve got work to do!” And they were, but they didn’t have quite the effect I’d intended. Mostly what they did was take up space and cause me to curse the fact that I still hadn’t finished that damn chest. Finally, I got fed up and took the three hours one evening to put the whole case together. It required a lot of drilling (by hand, because I wanted to make this as much by hand as possible), hammering, clamping, and holding awkward positions, but I got the case together. (See my last post for a bit more about this whole saga.)
Once the case was together, I sanded it smooth. No hand work this time, I used a power sander for sake of efficiency. Then it sat for another two weeks while I worked on some commissioned pieces and didn’t spend much other time in the shop. The only thing left to do was the lid. So last night I finished it. I chamfered the edges with a block plane, cut two battens out of a piece of 2×12 (using my band saw and planer to cut and mill them, because screw it, I’m running out of patience for this project!), then drilled the holes and nailed them to the lid. I clamped them on at first, then once the nails were driven I clenched them over with a few more hammer strokes. That way, even without glue the battens aren’t going anywhere, and seasonal wood movement won’t hurt anything. The pieces can all move freely, so hopefully nothing will crack.
Once the lid was finished, I sanded it, too. Then I went over the whole case and lid again with 2 more sanding passes. I had started with 80 grit, then moved up to 120 and 220 for the final pass. Once every surface was sanded, I pulled out my gloves, a rag, and my can of boiled linseed oil. Thirty minutes later, the lid and case were gleaming with a beautiful caramel glow. I put the rag outside on concrete to cure overnight after getting it wet with water (BLO can catch fire if you don’t have some way of removing the heat made by it curing). Then I showered and went to bed, exhausted but feeling incredibly good about myself.
Tonight I’m going to put on a second coat of oil. I might put a third on tomorrow, depending on how I feel about the color. After that, I’ll give it two days to cure completely and put a couple layers of paste wax on for the final protective coating. Since this will probably go in a bedroom of someplace else where it won’t take much abuse, I don’t expect it’ll need a polyurethane finish. I promise to post some pictures when it’s done. Until then, it’s still a top secret project.
Happy brewing (and building!)
Skål!

The ultimate hand tool: The Stanley No. 8 Jointer Plane. 10 lbs of cast iron heft and hubris. Seen here before I restored it to its original polished glory. Also seen here: The entropic hellhole that is the top of my workbench.
Over the past few months I’ve been doing a whole lot of work around my new house. Painting, putting up trim, installing towel racks. You know, those things you do after you buy a house to make it your own. On the plus side, this has meant that my house is now much more home-like and a lot less “all one awful beige color throughout.” On the minus side, until this past week I had spent very, very little time doing anything that I would consider “fun” work in my shop. Thankfully, that’s changed.
I’m a craftsman at heart. Sure, during the day I get paid to do math and write reports as an engineer, but my favorite days are those when I actually get to spend time in the lab or in a manufacturing plant actually DOING stuff. I’m the kind of person who needs to have their hands dirty and something tangible to show for the work they’ve done to be truly happy. That’s why over the last week I’ve finally made some time in my shop to actually get some real work done.
I have a large backlog of projects at the moment, something that I’m sure many of you understand. So many things to do, so little time, and all that. The problem I have is that when my backlog gets too big, I start to get overwhelmed by everything that I “have to” do. Suddenly, all those projects go from things I *want* to do to things I *must* do in my head. Since they’re things I must do, and obviously haven’t, I feel like I’m letting myself and my friends (who are inevitably the ones I agree to do projects for) down.
As anyone who’s ever been in this situation knows, that feeling of letting people down is the worst. Thing. Ever. Sure, there are worse things that can happen to you, and worse feelings, but when you’re in that black pit of why-did-I-agree-to-do-all-this-now-I’m-a-failure, it’s pretty hard to imagine anything worse. So what’s to be done? How to get yourself out of that funk?
Simple: Get back in the shop and MAKE STUFF.
No, really. It is that simple. The cure for the procrastination blues is to just. Start. Working.
Okay, maybe it’s a bit more complicated than that, but not much. Start off with something small and manageable. Something that you can get done in an evening for immediate gratification. In my case, I had a blanket chest that I’d started working on almost a year ago for an old friend. It was supposed to be a wedding gift for him and his wife. The wedding was ten months ago. I had thought to get it done quickly and have it for them. I was wrong. The work took longer and was more difficult than I first thought. So I put it away for awhile. But as the pieces sat in a stack in my basement for months, mocking me, that chest became a symbol for all the other things I had yet to do. So I finally set aside three hours last week and just put the case together. Drilled the holes, drove the nails, and trimmed the ends of the case flush. And at the end of the evening? I was hot, sweaty, and exhausted.
It felt amazing. I was excited, happy, and wanted to stay up for hours to keep working. But I went to bed, because it was almost midnight. The next day I did more work, and then I’ve kept doing work in my shop over the next few days since. I’m still not done with all the work on that blanket chest, but it’s very nearly done. Since then I’ve worked on a few other small items that people have asked me to make (and that I’m even getting paid for!), and have a lot of them in the shop now. They stand as encouragement, and testament to what actually putting excuses aside and DOING something can do for your mood and self-esteem.
I’ve got a lot of work left to do, that’s for certain. And I need to make sure I keep working at it in small bites. Otherwise I’m liable to fall back into my funk of self-defeating self-loathing. So if you need me I’ll be in the shop, making some more sawdust. It’s the best form of therapy I know.
Until next time, happy brewing (and sawing!).
Skål!
I’m going to rant a bit. I spent a couple hours tonight brewing what promises to be a rather tasty IPA, and I’m tired. I sit down at my computer to do a little reading before bed, and this story pops up.
Okay, Florida…
Let’s say, just for sake of argument, that I’m in a mood to be charitable with Florida Republicans tonight (Protip: I’m not, except for State Sen. Jack Latvala, R-Clearwater. He’s fighting this bill. I’m shocked, amazed, and quite pleased. That’s a conservative I can support! At least regarding this). At best, SB 1714 is a flagrant example of more burdensome regulations that they’re always decrying. At worst, it’s flagrant cronyism and pandering to special interests who’ve lined their campaign coffers with cash via PACs (beer distributors and large beer producers in particular).
It does not benefit consumers in any way whatsoever to force small producers like brewpubs to be forced to go through distributors. All it will do is force brewpubs to raise prices for consumers, to the detriment of their sales and bottom lines. In every other state that I’ve been to that has brewpubs, they’re allowed to sell their products directly to consumers on-site at said brewpubs. HOWEVER, if they want to sell in liquor stores, then they generally have to go through the same 3-tiered distribution system that every other producer uses to sell to the general public.
Personally, I think this system (being able to sell direct only from their own location) is just fine. They (the brewpubs) have gone to the trouble of setting up shop in-state, employing locals, paying local taxes and permit fees, etc. I think they deserve a bit of a break for that. Of course, if AB-InBev decides to build a multi-million dollar brewery down the road, then they should also be able to sell directly to consumers-at that brewery only. Distribution to liquor stores would still be through independent distributors. Here again, it’s only fair.
Republicans constantly claim to be the party of business, but also to be looking out for the best interests of their constituents. In this bill, their true colors are revealed. They certainly do care about their constituents. It just turns out that their constituents are the large corporations willing to pay big dollars to support their re-election campaigns. Ideas of fairness, equity, and the value of small local businesses over large chains doesn’t enter into their thinking at all. And their platitudes about the “free” market are as empty as the growlers in Florida brewpubs soon will be if this bill becomes law.
People of Florida, call your state reps and senators. Let them know that SB 1714 is unfair to local businesses, bad for the Florida economy, and bad for innovation in the craft beer market. If the big breweries are afraid of the little guys beating them out, maybe they should actually engage in, oh, I don’t know, making a better product instead of attempting to rig the system.
Because after all, isn’t that what capitalism is supposed to be about? Support fairness, Florida. Reward investment in local economies by small, independent brewpubs. Kill SB 1714. Keep craft beer flowing in Florida!
Skål!
P.S.- Someone go buy Sen. Latvala a beer. I don’t know much about his other political views, but he’s on the right side of this one in my book, and it seems like his heart is mostly in the right place.
You see that Corgi? That look of pure, unadulterated joy and excitement? He knows he is about to be thrown his ball. He is excited for his ball. He wants his ball. He’s bouncing off the floor repeatedly, begging for his ball. “OH EM GEE GIMMEH TEH BALL!!!!!1!” he shouts!
That is how I feel this afternoon. Tonight, for the first time in quite awhile, I will be brewing beer. Not for myself, but with some friends. There will be beer made. There will be beer consumed. And there will be good times had.
For me, the act of brewing is almost a religious experience. It’s the same ritual every time. Sure, the exact particulars vary from batch to batch, but the overall steps are the same. First, the grains are selected and ground, then mixed with hot water and allowed to steep. Then, while the grains steep, more water is heated for sparging. The grains are sparged and drained to extract the sugar, and the resulting wort is put on the burner to boil. Once boiling, the hops are added at specific times, along with any other special ingredients or finings that may be required. Then the beer is cooled and the gravity checked. Then comes the most critical step: The Adding Of The Yeast. If not done right, this step can go horribly wrong and the beer will be bad. But, if done right, the beer will be wonderful. If every other step is done right, from sanitizing to hop additions, the beer will be at least drinkable (there is, after all, no accounting for taste).
I get a great deal of satisfaction from drinking a good beer, regardless of whether or not I made it. Knowing the care and work that go into making a good product, especially as an engineer, helps me to appreciate them on an entirely different level than I think I otherwise could.
Now, with all that said, I’m going to go home, make dinner, and then go make some beer.
Skål!